An alternative to using a compensating leg to subtract gas pressure inside an enclosed vessel is to simply use a second pressure transmitter and electronically subtract the two pressures in a computing device:
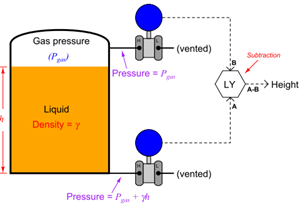
This approach enjoys the distinct advantage of avoiding a potentially wet compensating leg, but suffers the disadvantages of extra cost and greater error due to the potential calibration drift of two transmitters rather than just one. Such a system is also impractical in applications where the gas pressure is substantial compared to the hydrostatic (elevation head) pressure. If we add a third pressure transmitter to this system, located a known distance (x) above the bottom transmitter, we have all the pieces necessary for what is called a tank expert system. These systems are used on large storage tanks operating at or near atmospheric pressure, and can measure infer liquid height, liquid density, total liquid volume, and total liquid mass stored in the tank:
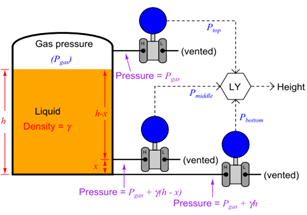
The pressure difference between the bottom and middle transmitters will change only if the liquid density changes since the two transmitters are separated by a known and fixed height difference.
Algebraic manipulation shows us how the measured pressures may be used by the level computer (LY) to continuously calculate the liquid density (γ):
P bottom − P middle = (P gas + γh) − [P gas + γ(h − x)]
P bottom − P middle = P gas + γh − P gas − γ(h − x)
P bottom − P middle = P gas + γh − P gas − γh + γx
P bottom − P middle = γx
P bottom − P middle/x = γ
Once the computer knows the value of γ, it may calculate the height of liquid in the tank with great accuracy based on the pressure measurements taken by the bottom and top transmitters:
P bottom − P top = (P gas + γh) − P gas
P bottom − P top = γh
P bottom − P top/γ = h
With all the computing power available in the LY, it is possible to characterize the tank such that this height measurement converts to a precise volume measurement (V ), which may then be converted into a total mass (m) measurement based on the mass density of the liquid (ρ) and the acceleration of gravity (g). First, the computer calculates mass density based on the proportionality between mass and weight (shown here starting with the equivalence between the two forms of the hydrostatic pressure formula):
ρgh = γh, => ρg = γ Then, ρ = γ / g
Armed with the mass density of the liquid inside the tank, the computer may now calculate the total liquid mass stored inside the tank: m = ρV
Dimensional analysis shows how units of mass density and volume cancel to yield only units of mass in this last equation: [kg] = [kg / m³] / m³
The accurate measurement of liquids in storage tanks is not just useful for process operations, but also for conducting business affairs. Whether the liquid represents raw material purchased from a supplier, or a processed product ready to be pumped out to a customer, both parties have a vested interest in knowing the exact quantity of liquid bought or sold. Measurement applications such as this are known as custody transfers because they represent the transfer of custody (ownership) of a substance exchanged in a business agreement. In some instances, both buyer and seller operate and maintain their own custody transfer instrumentation, while in other instances there is but one instrument, the calibration of which is validated by a neutral party.
List of Prominent Suppliers: Aquas, Ametek, Anderson Negele, Aplisens, Autosen, BCM Sensor, Endress + Hauser, Flowtech, HolyKell, Huba Control, Jiucheng, Keller, LEEG, LTH Electronics, Nivelco, Noshok, Piezus, Prisma, Scaime, VEGA, ZHYQ